Variational quantum algorithms are hard to train

Variational quantum algorithms

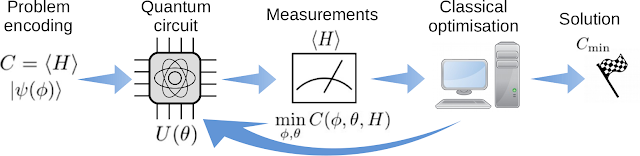
Variational quantum algorithms are an approach to solving hard optimization problems using quantum computers. Variational quantum algorithms encode the cost function describing the problem to be solved as the expectation value of a quantum Hamiltonian. A parameterized quantum circuit generates a trial solution to the problem, whose cost function is measured. Then, a classical computer trains the circuit parameters to reduce the cost function in order to find the optimal (lowest cost) solution to the problem.

Variational quantum algorithms are attracting a lot of interest owing to their ability to be run on near-term quantum processors. In particular, they have much lower circuit depths compared to algorithms designed for fault-tolerant quantum computers, and the iterative optimisation of the circuit parameters enables a robustness to errors in the individual quantum gates. However, there is no guarantee they will produce a good solution to the problem at hand, and in many cases there exist classical heuristic algorithms with provably better performance. In some cases, the problem encoding leads to a cost function described by a strongly-interacting or non-local quantum Hamiltonian for which finding the ground state (optimal solution) is provably hard to solve, even for a fault-tolerant quantum computer.

Training Variational Quantum Algorithms Is NP-Hard

An article just published in Physical Review Letters proves that, independent of the details of the quantum Hamiltonian encoding the problem, the classical optimisation part of variational quantum algorithms is NP-Hard to solve, meaning that the training step in which the quantum circuit parameters are adjusted exhibits many sub-optimal local minima which can trap commonly-employed gradient-based training methods. To show this, the authors considered a continuous version of the NP-Hard MaxCut problem that treats the quantum computer as an oracle that can efficiently generate and return expectation values of parameterised quantum states. Considering the simplest case where the problem Hamiltonian is diagonal in the computational basis is already sufficient to prove that variationally finding the optimal parameters for the quantum circuit is NP-Hard. Moreover, the optimisation in NP-Hard even for small quantum computers with logarithmically many qubits and non-interacting Hamiltonians; the difficulty does not rely on the hardness of the quantum ground state problem.

Perspectives

While this is definitely a sobering result for the field, rigorous results such as this are important in establishing the capabilities and limits of algorithms for near-term quantum computers and identifying possible methods to improve their performance. In this case, the hardness of the classical optimisation problem rests in the existence of many sub-optimal local minima; therefore developing heuristic strategies for generating good initial guesses that are sufficiently close to good solutions should be a priority. Another promising point the authors raise is that this hardness result is similar to the hardness of the Hartree-Fock method routinely employed in quantum chemistry; even though this related problem is NP-Hard, it is still useful as a starting point for many practical quantum chemistry calculations. We can hope to draw inspiration from methods to obtain good initial guesses that quantum chemists have spent decades perfecting.

Questions to ask before trying to solve your hard classical optimisation problem on cloud quantum computers

• Do my problem encoding and parameterized circuit design avoid the barren plateau problem?
• Do I have a method to choose a reasonable initial guess for my circuit parameters, e.g. using perturbation theory or a mean field solution? Random initial guesses are highly unlikely to converge.
  
• How many qubits do I need to solve problem instances that are too large for existing classical solvers? Can I use a qubit-efficient problem encoding?